In this article I will go through all you need to know for Physics AS on Chapter 2. This will include going over in order (I think!) current, flow of charge per second, voltage (or potential difference), resistance in series and parallel, potential dividers, internal resistance and EMF of a power supply, power calculations, work done, conductance, resistivity and conductivity.
Current
An electric current is a flow of charge.
When we connect a wire up to a battery, negatively charged particles (electrons) flow through the wire from the negative end of the battery to the positive end. We call this flow of charge an electric current, and, as you know, the charge will only flow if there is a complete circuit. The electric current at a point in the wire can be defined in the following ways:
- I = nq – where I = current in Amps, n = number of charged carriers per second and q = the charge on one charge carrier. Rearrangements are as follows n = I/q and q = I/n.
- I = Q/t – where I again is current in Amps, Q = charge in coulombs and t = time in seconds. Rearrangements are as follows Q = It and t = Q/I.
Voltage (Potential Difference)
- The amount of energy it is given by the power supply is the voltage across the power supply.
- The amount of energy it gives to each individual component in the circuit is the voltage across the component.
V = E/Q – where V = voltage in volts, E = energy in joules and Q = charge in coulombs. Rearrangements of this formula are as follows Q = E/V and E = VQ.
Resistance
Generally speaking, when there is a voltage across a component there will be a current through it. Usually, as the voltage increased the current increases – this makes sense if you think of the voltage as a kind of force pushing charged particles. We formalise the relationship between current and voltage by introducing the idea of ‘resistance’:
R = V/I – where R = resistance in ohms, V = voltage in volts and I = current in amps. Rearrangements of this formula are as follows V = IR (notice how it has the same format as y= mx, a line equation for a graph. This makes R the constant and gradient on the graph or V= IR) and I = V/R.
 It is important to know how to work out the resistance of different resistors in parallel and in series.
It is important to know how to work out the resistance of different resistors in parallel and in series.
Resistors in Series
Rt = R1 + R2 – where Rt = Resistance Total
This is a simple equation where you add up each resistor to make the total resistance.

Resistance in Parallel
1/Rt = 1/R1 + 1/R2
This is a little more trick as there are reciprocals in this equation. Working out 1/R1 + 1/R2 should be easy. The mistake most people do though is to forget to do one over (1/R1 +1/R2). For example, if you worked out 1/R1 + 1/R2 was 5, the answer is not 5. Your left with 1/Rt = 5 meaning you have to do 1/5 to get the answer which is 0.2 Ohms.
Potential Dividers
How is voltage shared between components in a circuit? Through using Ohms law V = IR.
We will use an example with the diagram below:
Voltage 1 / Total Voltage = Resistance 1 / Total Resistance
or…
V1 / Vs = R1 / Rt – where Vs = Voltage Supply (total voltage_ and Rt = Total Resistance be it in series (Rt = R1+R2 etc..) or parallel (1/Rt = 1/R1 +1/R2 etc…).
This gives us a rearranged formula of…
V1 = Vs (R1 / R1 + R2)
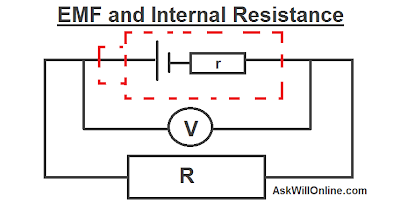
Internal Resistance + EMF
The internal resistance, r, is the resistance associated with the internal workings of a power supply. Because it is internal to the power supply, you can not measure it directly.
The electromotive force (e.m.f) is the ideal potential difference associated with a power supply. It’s what you would measure if the internal resistance were zero.
The terminal potential difference is the actual potential difference measured across the two terminals of a power supply. It will always be less than the electromotive force due to the effect of internal resistance.
The lost volts is the potential difference across the internal resistance. It depends on the electromotive force (EMF) and the circuit the power supply is connected to.
The key is to know that with any power supply, there is always a resistance internally in the power supply. This resistance could be negligible (near to nothing) or quite a lot. If there is a resistance, the circuit can be seen as a potential divider if there is another resistor in the circuit.
Vt = EMF -Vr (Vr is lost volts) which is the same as Vt = E-Ir
We can also used V = IR:
- V = I x R
- I = V / R + r (r is internal resistance)
- I = EMF / R + r
- I = Total Voltage / Total Resistance
P = VI – where P = power in watts, V = voltage in volts and I = current in amps
W = QV – where W = work done in Joules, Q = charge in coulombs and V = voltage in volts
Resistance and Conductance
- “A good electrical conductor has low resistance”.
- “A large current for a small voltage”.
R = 1 / G and G = 1 / R
This means that if R = V / I, G must equal I / V .
Measurement of Conductance
We know that Resistance (R) is measured in Ohms (Ω). If G = 1 /R, the unit for G must be 1 / Ω or Ω-1. This unit is more known as Siemens (S):
1 S = 1 / Ω
Example
An unknowing resistor has a current of 0.2mA flowing through it when a voltage of 7.6 V is placed across it. Work out the resistance conductance of the resistor.
- Resistance = V / I which equals 7.6 / 2 x 10-4 (remember that it’s milliamp!) = 38,000 Ω or 38k Ω.
- Conductance = I / V which equals 2.6 x 10-5 S.
- Rt = R1 + R2 etc… in series, then the Conductance is the reciprocal of that at 1/Gt = 1/G1 + 1/G2 etc…
- 1/Rt = 1/R1 + 1/R2 etc… in parallel, then the Conductance is the reciprocal of that at Gt = G1 + G2 etc…
Resistivity and Conductivity
Resistivity = Resistance x Cross-sectional Area / original length
With the use of symbols, this is…
ρ = R A /
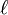 = length and is measured in meters
= length and is measured in metersR = ρ
/ A
Conductivity (σ, sigma) = 1 / ρ
This makes the equation…
σ = G
/ A
Where σ = conductivity and is measured in Siemens per metre, G = Conductivity, 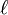 = original length and A = Cross Sectional Area.
= original length and A = Cross Sectional Area.
This equations are pretty difficult to learn. However, a good way to remember conductivity and conductance is through the rearrangement of the above formula:
G = σ A /
Which funnily enough spells out Goal! This equation is centred around conductance and can be arranged again to centre around conductivity or sigma (σ).
It’s a lot to take in so if you are stuck on any of it, please comment below, subscribe to future comments and I will try my best to answer your questions. Hope this has helped! Please also see other revision material I have done on Physics AS.